Disclaimer: The tricks mentioned below are NOT a substitute for learning the material. Apply these tricks only as a last resort. Note that we will focus on the Business Mathematics and Logical Reasoning & Statistics paper in the CA Foundation course. But, you can adapt them to any field.
In our humble opinion, the Business Mathematics and Logical Reasoning & Statistics paper should be solved easily. After all, the level of the paper is no higher than 11 or 12th grade mathematics.
Having said that, we’ve noticed that students do face difficulty with this paper – either because they are scared of mathematics, or took it too easily. Another reason may be because they don’t know how to take advantage of their knowledge! Or didn’t manage their time well.
We think it’s time to give you a new perspective on the paper. And how to gain a few extra marks that you may not have gotten before!
Without further ado, here are 4 tricks to help you ace that MCQ. We’ll use the mock test released by ICAI for examples where we put these methods to good use. We suggest that you have the test paper handy. Also, don’t forget to sign up for our online video lectures and see how our professors tackle MCQs!
4 Tricks to Ace that MCQ
Tip 1: Elimination Method
This method involves guessing intelligently. Yes, we know, there’s negative marking in this paper. Yes, it’s foolish to guess when you have no knowledge. But suppose you do know something about something. It would be foolish to NOT put this to good use, yeah? And also, if it so happens that you are tackling an MCQ with no negative marking, then guess away even if you don’t know anything! (For example, in the CS Foundation papers, all papers are MCQ based with no negative marking.)
We mean to say that this elimination method works best if you have pre-existing knowledge about the subject.
Let’s see how this works with the help of a couple of examples.
Example 1.1
Remember we told you to keep the paper handy? Open it now and scroll down to question 30.

Now, it can’t be (a) because we know that there are non-zero matrices whose determinants are 0. For example, a matrix like
1 1
1 1
Has determinant 0.
And option (d) doesn’t make sense.
We can cross off (a) and (d)
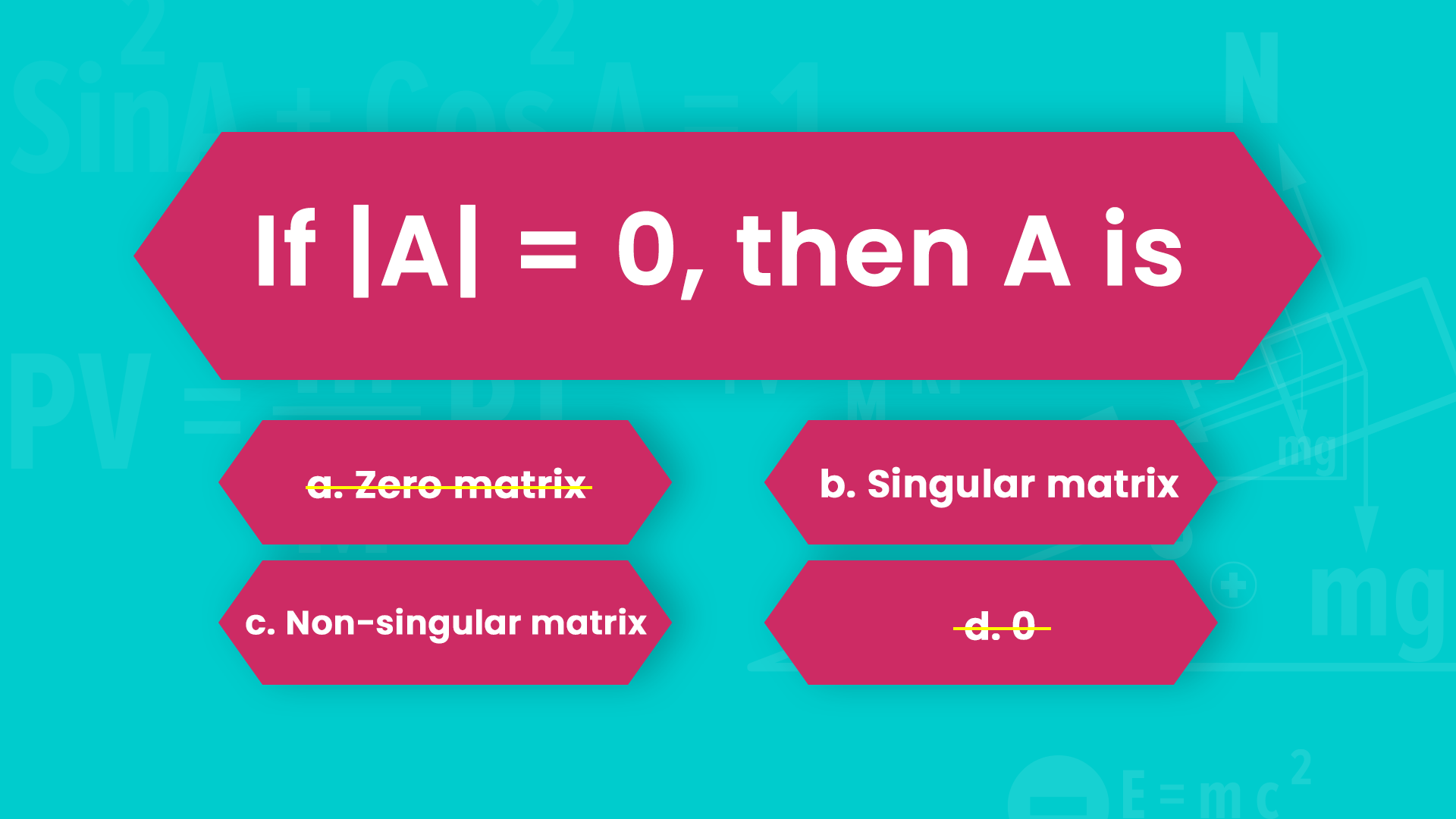
The option has to be either (b) or (c). Guess from among the two choices and move on! You have a fifty percent chance of getting it right. And with a negative marking of -0.25, it’s worth taking the risk.
Example 1.2
This is question 74.
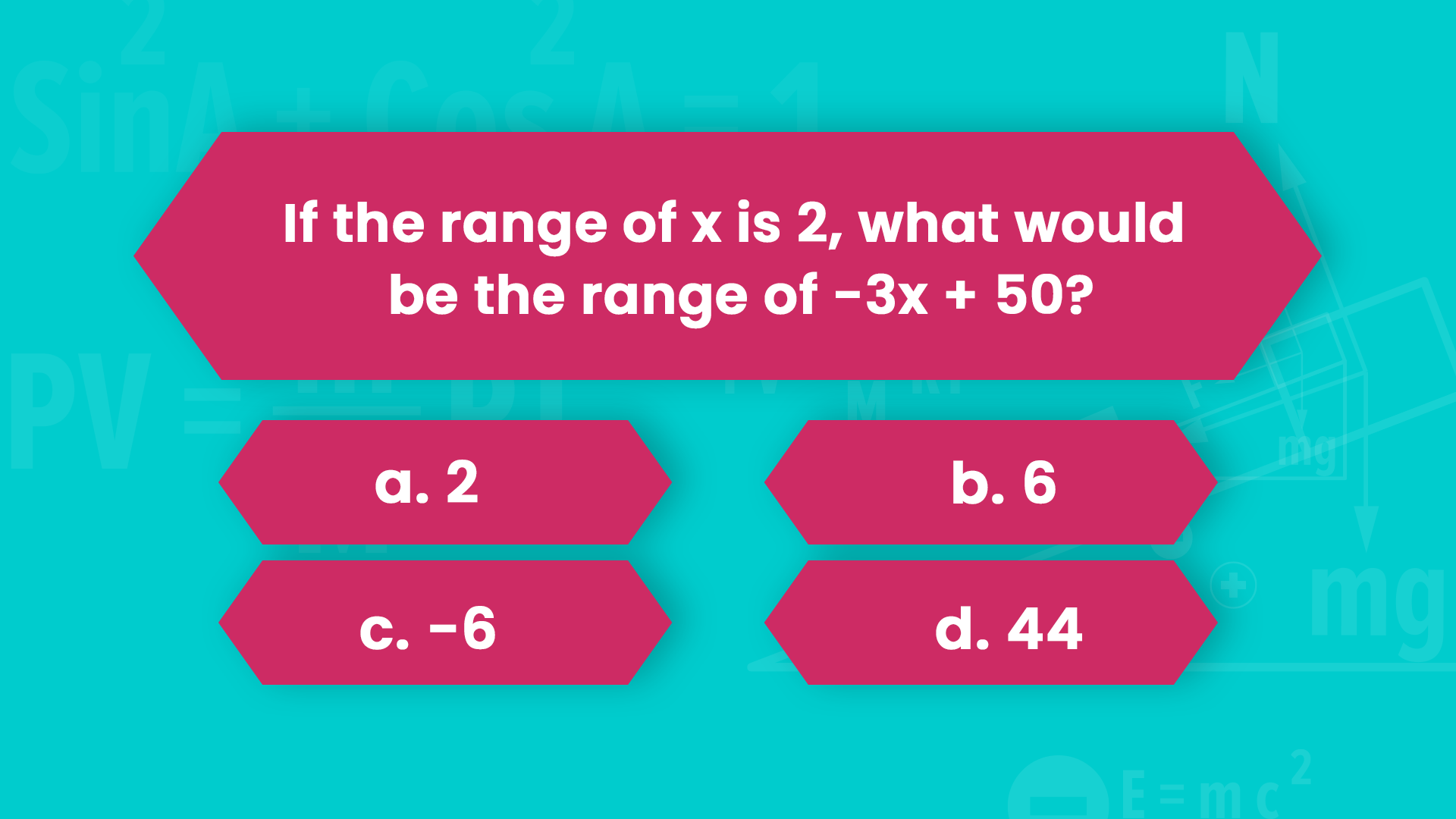
Again, if you only remember one thing about ranges, that is, it has to be positive, you can remove (c) and guess from the remaining three.
Get the point?
We invite you to practice this elimination method on other examples in the test that you know nothing about.
Go ahead give it a try. You’ll be surprised to see how many marks you’ll gain!
| Did you know? |
| You can perhaps do better if you get into the minds of the question setter. The setter knows that if people are in a hurry, they tend to get careless. One careless mistake people often make is that they mess up signs. That is suppose they calculate the answer as 3. They might mark the option that says -3 in the paper by mistake if they are going fast! So, without calculating the range, and getting into the mind of the tester, what do you think the answer for question 74 would be? Tell us in the comment section below! |
Tip 2: Look at the Answer Choices First
This tip is similar to the elimination method. It adds to it though! It works like this:
For example, suppose the question involves setting up and solving a lot of tedious equations.
Before doing any set up and calculations, it’s a good idea to look at the answer choices first. And see if the answer pops out right away!
Let’s look at a couple of examples so that you understand what we mean.
Example 2.1:
Jump to question 25. The question says:

Now before setting up the equation to solve the problem, notice the phrase: “the digit in the tens place is 3 times the digit in the unit’s place”
From that info, only 93 fits the bill, right?
And to check it’s 93, we see that 93 – 54 = 39. Digits reversed.
Done.
Compare this to the standard way:
Let z be the number. Let x be the unit’s digit, y the ten’s digit.
That is z = 10y + x
From the question, we see y = 3x. (Digits in the tens place is 3 times the digit in the unit’s place.)
So, z = 31x.
Also the question says that if 54 is subtracted from the number, the digits are reversed.
So z – 54 = 10x + y = 13x (because y = 3x)
Which means z = 13x + 54
But from above, we see 31x = 13x + 54
= > 18x = 54 which means x = 3
And therefore y = 9.
And so, z = 9*10 + 3 = 93.
Looooooooooong and tedious right? So much faster if you use “common sense”!
Example 2.2
Go to question 27.

At first glance, you might think that you’d have to figure out the pattern to come up with the relationship!
No need. Again the answer choices will give you a clue.
Let’s look at the first column:
y = 11 when x = 5.
Look at option (a). What’s y when x = 5?
Yep. Not 11.
Option b?
No, not 11.
Option (c)?
Yes! 11. So circle (c) and move on?
Not so fast. It’s a good idea to check (d) first.
Okay. In this case, it’s not 11. It can’t be (d). Has to be (c) and now you can move on.
Wait. Before we move to the next tip, let’s change the options to this question slightly.
What if option (c) was y = 3x – 4? And option (d) was y = 2x + 1?
That is the question reads thus:

If you used this method without thinking, you’d have seen that y = 3x – 4 would yield 11 when x = 5. And you’d have chosen (c) and moved on!
But it’s not (c) because if you look at the second column, you see that the equation wouldn’t fit. That is if x = 6, your solution would yield y = 14. It should be 13 according to the table.
Wrong answer!
That’s why, for the best use of this method, look at ALL the answer choices before making your choice.
| Did you know? |
|
A variant of this method is called plugging in. (or substitution). A simple example is something like this: What’s the integer solution to the equation x3 – 5x + 2 = 0?
If you check the answer choices one by one, you see it’s option (b) or 2(!). No need to try and solve this horrible cubic equation! |
Tip 3: Drawing a Picture
You know the old saying, “a picture is worth a thousand words.”? We think, in this case, a picture is worth a thousand calculations!
It’s a good idea to draw pictures to solve mathematical problems! Even logical questions.
Again, let’s look at an example. Because you know that an example is worth a thousand words.
Before we get into the example, why don’t you download our mobile app? Our faculty Supritha Marla, in the subject Business Mathematics, Logical Reasoning and Statistics, solves problems using this method!
Example 3.1
Question 15 in the paper.

To solve this, draw a pic.
You know that to check the properties of a relation, you need to have three members of the set.
The set under investigation is the set of lines in the plane.
Let’s take 3 lines, AB, CD and EF.
We are checking the relation “is perpendicular to”.
So let’s take CD perpendicular to AB and AB perpendicular to EF as shown:
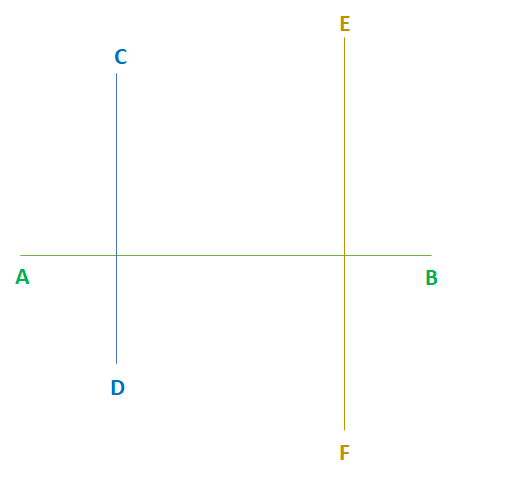
Let’s check for reflexitivity. Is AB perpendicular to itself? No way! It’s parallel to itself not perpendicular.
The relation is not reflexive.
Let’s check for transitivity.
We know that CD is perpendicular to AB. We also know AB perpendicular to EF. Does it follow then that CD is perpendicular to EF? That is, is the relation transitive?
From the diagram, we see it’s not!
Only thing left is to check for symmetry. Is it true that if CD is perpendicular to AB, then AB is perpendicular to CD? Clearly, yes.
It’s a symmetric relation.
(b) is correct!
Let’s look at another example.
Example 3.2
Example 58 from the paper:

Statements: Some ships are boats. All boats are submarines. Some submarines are yachts.
We know you can try to follow the logic and figure out the answer. But there’s a much easier way! Draw a pic!
Venn diagrams come to your rescue here.
There are four sets in consideration right?
Set of ships, boats, submarines and yachts.
First statement:
Some ships are boats.
Let’s put this in Venn diagram form thus:

Why like this? Because the intersection between the two sets is not empty. (Some ships are boats.)
We don’t know if one is a subset of the other; not specified so far. So this is the best representation of the information we have so far.
Now, we see that all boats are submarines. That is a boat is a subset of the submarine set.
There are two possibilities:
Possibility 1:

Possibility 2:

Let’s keep both in mind for now.
Third statement:
Some submarines are yachts.
There are now many possibilities. Here are three ways this could fit the diagram:
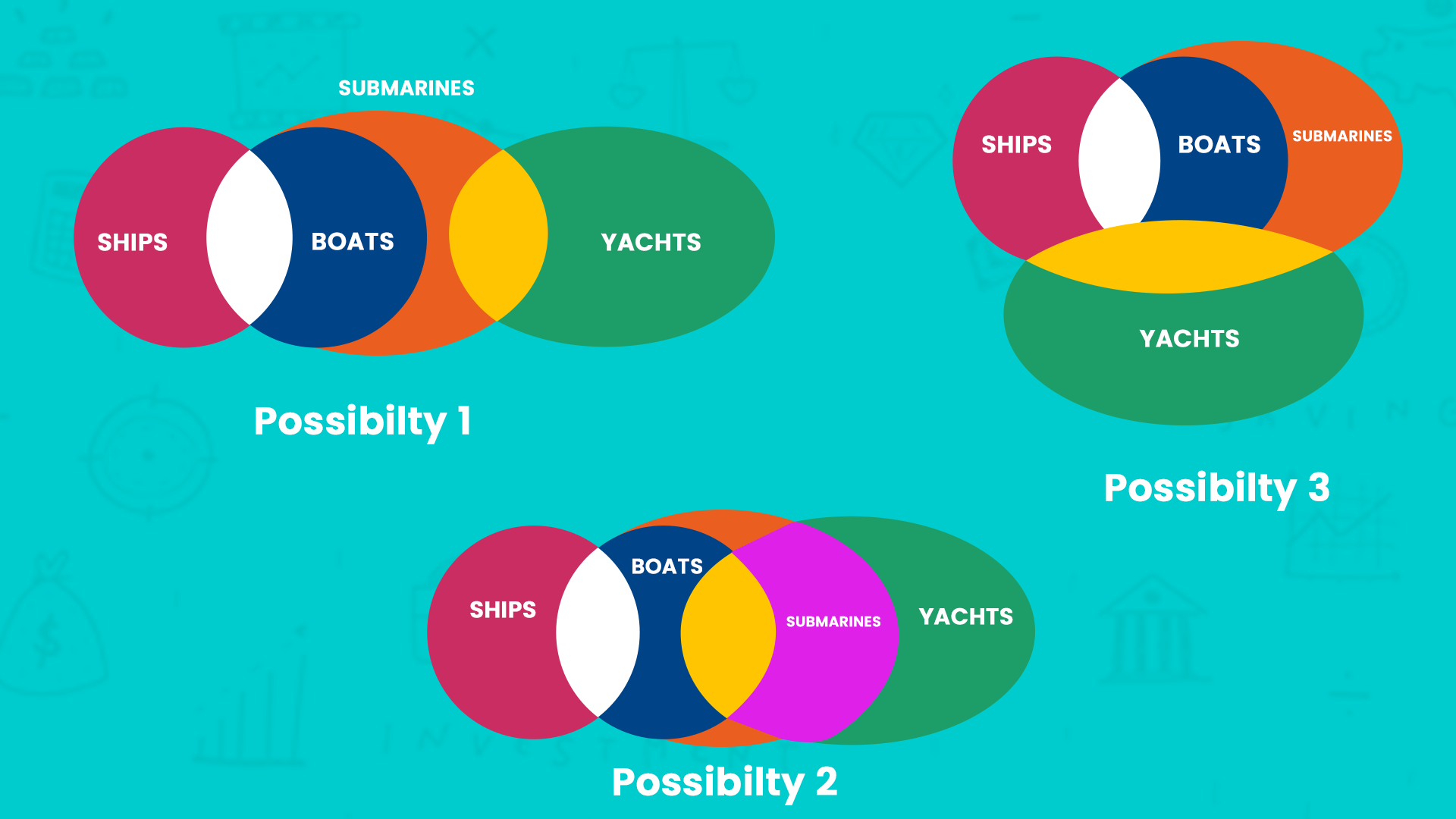
Now let’s look at the conclusions.
Conclusion I: Some yachts are boats.
Does this follow? From our diagram, no! Because you could lie in possibility one above. So I doesn’t necessarily follow.
Conclusion II: Some submarines are boats.
Is the intersection between the set of boats and set of submarines empty? In any conceivable possibility? No! In every case, the intersection between the sets of boats and submarines is non-empty.
Exercise for the reader: Try drawing the Venn diagram for all possibilities. You will see that in every case, some submarines are definitely boats
We conclude II is correct.
Let’s look at III.
Conclusion III: Some submarines are ships.
This is clearly true because no matter what diagram we draw, the intersection between the set of submarines and set of ships is always non-empty.
Conclusion IV: Some yachts are ships.
Can we conclude this from the diagram? Not really. It doesn’t follow!
So only II and III have to be correct. I and IV may or may not be. More information needed.
We circle option (b) and move on.
See how a pic helps?
Do you really want to follow the logic when a Venn diagram comes in handy?
Now, don’t worry if you don’t completely understand how to solve this question. As mentioned earlier, our faculty Supritha Marla for the subject solves questions like these step by step.
Tip 4: Slowing Down
Yes. It’s good to slow down. And this goes hand in hand with one of the previous tips. Look at all the answer choices first before making your decision
Only one example this time. This is a question we made up. By the way, assume that the instructions at the top of the exam says, choose the best answer.

If you rush, you’d pick (a) and be done with it, yeah? But if you read the options carefully, you’ll see that the answer is (d)!
And we told you yet another example of where if you rush, you miss out. (See tip 2).
Bonus Trick
Okay, as promised we gave you four cool tips. But because we like you, we want to give you a super advanced top-secret tip!
Sometimes you can find a clue to an answer to a question on the test from another question!
Yep. You read that right.
Don’t believe us? Let’s look at the paper again.
Let’s go to question 29.
It says:

Okay, okay. We know this is easy and you wizards will get it quick. But we just wanted to illustrate a point, you see.
Let’s assume that you have no idea. And you’ve left this blank. And have gone further ahead.
You come across question 31:

And again, let’s assume that once again, you’ve forgotten this concept.
But can you use both these questions to get the answer for both? Or least eliminate a choice?
Yes!
Let’s analyse both questions:
The first asks what’s the condition for multiplying matrices and the second says that if two matrices are multiplied, what would be the order?
Clearly, in the second question, two matrices of different orders are multiplied together.
But wait. Option (b) in question 29 says that two matrices can be multiplied only if they are of the same order. The second question contradicts this answer!
So, you can eliminate option (b) in question 29(!).
If you can’t proceed further, this is a win, right? At least now, you can make an educated guess for question 29.
Final Thoughts
This just about wraps it up for this blog. We want to close by saying that don’t take these tips in isolation. You can use multiple techniques to solve a question!
Also, we want to emphasise that you MUST prepare yourself thoroughly before the exam. You don’t want to be in a position where you’ve to keep making educated guesses for every question. There’s no substitute for good prep!
Found these tips useful? We invite you to sign up for our courses where you can put these tips to good use. Also try your hand at some mock questions in our study material and see how you fare.



